『목차』
0. 개요
1. 문제
2. 풀이
3. 코드
0. 개요
터렛을 가장한, 두 원의 위치관계를 묻는 문제이다. 지문에는 4명의 인물 '이석원, 조규현, 백승환, 류재명'이 등장하는데, 이석원은 아무런 역할을 하지 않는다...(?!) 조규현과 백승환은 원의 중심을 나타내고, 류재명까지의 거리는 원의 반지름을 나타내는데 말이다. 학창 시절에 공부한 두 원의 위치관계를 떠올리면 문제는 쉽게 풀린다. 잘 모르겠으면, 두 원의 위치관계에 대해 구글링을 해보자. 기억이 새록새록 날 것이다.
1. 문제
https://www.acmicpc.net/problem/1002
1002번: 터렛
각 테스트 케이스마다 류재명이 있을 수 있는 위치의 수를 출력한다. 만약 류재명이 있을 수 있는 위치의 개수가 무한대일 경우에는 -1을 출력한다.
www.acmicpc.net
[문제]
조규현과 백승환은 터렛에 근무하는 직원이다. 하지만 워낙 존재감이 없어서 인구수는 차지하지 않는다. 다음은 조규현과 백승환의 사진이다.

이석원은 조규현과 백승환에게 상대편 마린(류재명)의 위치를 계산하라는 명령을 내렸다. 조규현과 백승환은 각각 자신의 터렛 위치에서 현재 적까지의 거리를 계산했다.
조규현의 좌표 (x1, y1)와 백승환의 좌표 (x2, y2)가 주어지고, 조규현이 계산한 류재명과의 거리 r1과 백승환이 계산한 류재명과의 거리 r2가 주어졌을 때, 류재명이 있을 수 있는 좌표의 수를 출력하는 프로그램을 작성하시오.
[입력]
첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 다음과 같이 이루어져 있다.
한 줄에 x1, y1, r1, x2, y2, r2가 주어진다. x1, y1, x2, y2는 -10,000보다 크거나 같고, 10,000보다 작거나 같은 정수이고, r1, r2는 10,000보다 작거나 같은 자연수이다.
[출력]
각 테스트 케이스마다 류재명이 있을 수 있는 위치의 수를 출력한다. 만약 류재명이 있을 수 있는 위치의 개수가 무한대일 경우에는 -1을 출력한다.
[예제 입력 1]
3
0 0 13 40 0 37
0 0 3 0 7 4
1 1 1 1 1 5
[예제 출력 1]
2
1
02. 풀이
[입력값의 이해]
조규현과 백승환의 위치는 원의 중심을 나타내고, 각각에서부터 류재명까지의 거리는 원의 반지름을 나타낸다.
∴ $x$, $y$는 원의 중심좌표, $r$은 반지름에 대한 정보를 나타낸다.
$x_1$, $y_1$, $r_1$은 첫번째 원에 대한 정보이고, $x_2$, $y_2$, $r_2$은 두번째 원에 대한 정보이다.
[출력값의 이해]
류재명이 있을 수 있는 위치는 결국, 조규환과 백승환의 위치를 중심으로 하는 두 원의 교점에 해당한다.
∴ 두 원의 위치관계를 통해 교점의 개수를 파악할 수 있고, 이는 류재명이 있을 수 있는 위치의 개수에 해당한다.
[두 원의 위치관계에 대한 이해]
두 원을 각각 $O$, $O'$라 하고, $O$의 반지름을 $r$, $O'$의 반지름을 $r'$, 두 원의 중심 사이의 거리를 $d$라 하자.
이때, 두 원이 일치하는 경우에만 교점의 수가 무한대가 된다는 점을 유의하도록 하자.
| 위치관계 | 교점수 [반환값] |
수식 | 그림 |
| 1-1. 두 원이 일치한다. | 무한대[-1] | - | - |
| 2-1. 만나지 않는다_외부 | 0[0] | $r+r'<d$ | 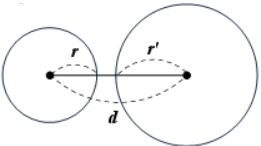 |
| 2-2. 한 점에서 만난다_외접 | 1[1] | $r+r'=d$ | 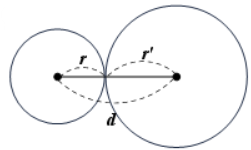 |
| 2-3. 두 점에서 만난다 | 2[2] | $|r-r'|<d<r+r'$ | 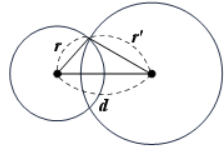 |
| 2-4. 한 점에서 만난다_내접 | 1[1] | $d<|r'-r|$ | 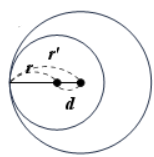 |
| 2-5. 만나지 않는다_내부 | 0[0] | $d<|r'-r|$ | 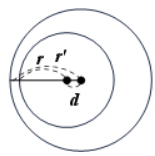 |
| 2-6. 만나지 않는다_동심원 | 0[0] | $d=0$ | 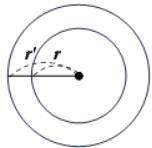 |
위에서 언급한 내용들을 가지고 코드를 구성하면 아래와 같다.
3. 코드
#pragma warning(disable:4996) //visual studio scanf 오류 방지.
#include <stdio.h>
#include <stdlib.h> //abs() 함수 사용 목적.
#include <math.h> //수학함수 사용 목적.
/* 원 구조체 선언 */
typedef struct {
int x;//x좌표
int y;//y좌표
int r;//반지름
}Circle;
/* 두 원의 중심 사이 거리 구하는 함수 */
double center_distance(Circle c1, Circle c2) {
return sqrt(pow(c1.x - c2.x, 2) + pow(c1.y - c2.y, 2));
}
/* 두 원의 위치관계 구하는 함수 */
int positional_relationship(Circle c1, Circle c2) {
double d = center_distance(c1, c2);//자료형이 double임에 주의.
/* 1. 두 원이 일치할 때 */
if (c1.x == c2.x && c1.y == c2.y && c1.r == c2.r) {
return -1;
}
/* 2. 두 원이 일치하지 않을 때 */
else {
/* 2-1. 외부 = 교점 0개 */
if (c1.r + c2.r < d)
return 0;
/* 2-2. 외접 = 교점 1개 */
else if (c1.r + c2.r == d)
return 1;
/* 2-3. 두점에서 만남 = 교점 2개 */
else if (abs(c1.r - c2.r) < d && d < c1.r + c2.r)
return 2;
/* 2-4. 내접 = 교점 1개 */
else if (abs(c1.r - c2.r) == d)
return 1;
/* 2-5. 내부 = 교점 0개 */
else if (d < abs(c1.r - c2.r))
return 0;
/* 2-6. 동심원 = 교점 0개 */
else if (d == 0)
return 0;
}
}
int main(int argc, char* argv[]) {
int T;
Circle c1, c2;
scanf("%d", &T);
for (int i = 0; i < T; i++) {
scanf("%d %d %d %d %d %d", &c1.x, &c1.y, &c1.r, &c2.x, &c2.y, &c2.r);
printf("%d\n", positional_relationship(c1, c2));
}
return 0;
}'⌨️CS-PS > 백준_기하' 카테고리의 다른 글
| [Baekjoon/백준][4153][C/C++] 직각삼각형 (0) | 2023.02.06 |
|---|---|
| [Baekjoon/백준][3009][C/C++] 네 번째 점 (0) | 2023.01.30 |
| [Baekjoon/백준][1085][C/C++] 직사각형에서 탈출 (0) | 2023.01.28 |

